El concepto de semejanza en la vida cotidiana
En lenguaje cotidiano, cuando se habla de semejanza , casi siempre se hace referencia al concepto más general de parecido : color “parecido”, tamaño “parecido”, forma “parecida”, etcétera.
En los ejemplos, el significado de semejanza que hacemos notar hace referencia a una característica común entre objetos o personas: color, tamaño y forma, entre otros.
El concepto de semejanza en matemática
En cambio, en matemática el concepto de semejanza está muy ligado al concepto de proporcionalidad ; por ello se dice que dos objetos son semejantes si "tienen" una proporción entre ellos.
Por ejemplo, un mapa es una representación semejante a una porción del globo terráqueo, de allí que deba tener una misma proporción, para que las medidas que se tomen sobre él sean lo más cercanas a su valor real.
Ahora, si tenemos dos anillos idénticos, cuyos diámetros son exactamente iguales, diremos que tienen la misma proporción y semejanza entre cada una de sus partes (circunferencia, radio, área, diámetro).
Si dos polígonos regulares tienen igual número de lados, entonces son semejantes.
Toda circunferencia es semejante a otra circunferencia.
La congruencia es un caso particular de la semejanza.
Semejanza de triángulos
En el estudio de la semejanza entre figuras planas , el tópico de la semejanza de triángulos es muy importante para quienes postulen a la PSU .
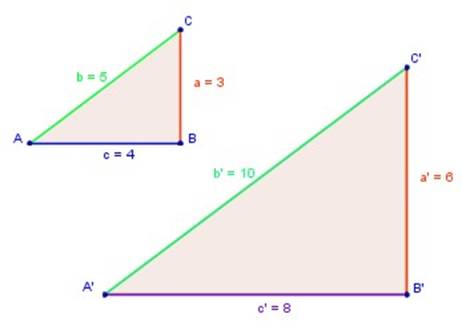
De modo general, diremos que dos triángulos son semejantes cuando los ángulos de uno de ellos sean respectivamente congruentes con los ángulos del otro y, además, tengan proporcionales sus lados homólogos (correspondientes).
Para avanzar en la comprensión del concepto de semejanza es preciso definir y entender qué son lados homólogos (correspondientes) y qué es proporcionalidad .
Tenemos la figura siguiente: