El conjunto de los números reales
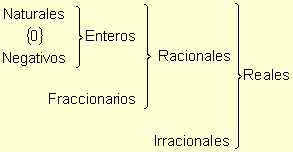
Al conjunto de los números reales se llega por sucesivas ampliaciones del campo numérico a partir de los números naturales. En cada una de las ampliaciones se avanza y mejora respecto de la anterior.
Con los números naturales (N) se puede sumar y multiplicar pero no se puede restar (a - b) si a < b. Se definen así los números negativos o enteros negativos que al unirse con el cero y los naturales constituyen el conjunto de los números enteros (Z). Con los números enteros (Z) se puede sumar, restar, multiplicar pero no dividir 
si a no es múltiplo de b.
Se definen así los números fraccionarios que unidos a los enteros constituyen el conjunto de los números racionales.
Todo número racional se puede expresar como un número decimal exacto 
o como un número decimal periódico, es decir con infinitas cifras decimales que se repiten 
Con los números racionales se puede sumar, restar, multiplicar y dividir ( si b ¹ 0). Si bien el conjunto de los números racionales tiene una muy buena estructura para realizar las diferentes operaciones quedan algunas situaciones que no se pueden considerar dentro de él (
,
, p , entre otros). Surgen los números irracionales para dar respuesta a estas instancias.
Los números irracionales se pueden expresar como números decimales de infinitas cifras decimales no periódicas.
Los números irracionales (I) unidos a los racionales (Q) definen el conjunto de los números reales (R).
Los números reales cumplen propiedades comprendidas en tres categorías: propiedades algebraicas, propiedades de orden y de completitud. Las propiedades algebraicas establecen que los números reales pueden ser sumados, restados, multiplicados y divididos (excepto por cero) obteniéndose otro número real.
Los números reales y la recta real
En la geometría analítica el paso importante fue establecer una correspondencia entre los números reales y los puntos de la recta. Existe una condición que cumplen los números reales llamada axioma de completitud que garantiza una correspondencia biunívoca (uno a uno) entre el conjunto de los números reales y el conjunto de puntos en la recta o eje. A cada número real le corresponde un único punto sobre la recta y a cada punto en la recta o eje se le asocia un único número real. Como se observa en el gráfico, se elige un punto de referencia arbitrario sobre la recta al que se denomina origen. Se selecciona además una unidad de longitud para medir distancias. Se elige también un sentido a lo largo de la recta a la que se llama positivo y se considera como negativo al sentido opuesto. A cada número real entonces se le asocia un punto de la recta teniendo en cuenta lo siguiente:
· se asocia al origen el número 0,
· se asocia a cada número positivo p un punto que está a una distancia de p unidades del origen en la dirección positiva,
· se asocia a cada número negativo - p el punto que está a p unidades de distancia del origen en la dirección negativa.
Los puntos en la recta se identifican con los números que representan. El número real que le corresponde a un punto de la recta se denomina coordenada o abscisa del punto y la recta recibe el nombre de recta real, recta coordenada, recta numérica o recta de los números reales. También se la conoce como eje coordenado o eje real.
El conjunto de los reales cubre o completa la recta sin dejar "huecos".
Ejemplo.
Orden
Los números reales están ordenados cumpliendo sólo una de las afirmaciones siguientes: dados dos números reales a y b puede ser que a sea menor que b, a sea mayor que b o a sea igual a b.
Puede observarse en la recta que a < b si y sólo si el punto que representa al número a está a la izquierda del punto que representa al número b.
Análogamente, a > b sí y sólo sí el punto que representa al número a se halla a la derecha del que representa a b.
Si a = b, los puntos se superponen.
La relación de orden queda establecida teniendo en cuenta que el punto a precede al punto b si el número real a es menor que el número real b (a < b).