Probabilidad

 Un árbol de probabilidad o diagrama de árbol es una herramienta que se utiliza para determinar si en realidad en el cálculo de muchas opciones se requiere conocer el número de objetos que forman parte del espacio muestral, estos se pueden determinar con la construcción de un diagrama de árbol.

El diagrama de árbol es una representación gráfica de los posibles resultados del experimento, el cual consta de una serie de pasos, donde cada uno de estos tiene un número infinito de maneras de ser llevado a cabo. Se utiliza en los problemas de conteo y probabilidad.

Para la construcción de un diagrama en árbol se partirá poniendo una rama para cada una de las posibilidades, acompañada de su probabilidad. Cada una de estas ramas se conoce como rama de primera generación.

En el final de cada rama de primera generación se constituye, un nudo del cual parten nuevas ramas conocidas como ramas de segunda generación, según las posibilidades del siguiente paso, salvo si el nudo representa un posible final del experimento (nudo final).

Hay que tener en cuenta que la construcción de un árbol no depende de tener el mismo número de ramas de segunda generación que salen de cada rama de primera generación y que la suma de probabilidades de las ramas de cada nudo ha de dar 1.

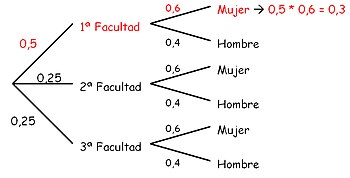
Existe un principio sencillo de los diagramas de árbol que hace que éstos sean mucho más útiles para los cálculos rápidos de probabilidad: multiplicamos las probabilidades si se trata de ramas adyacentes (contiguas), el ejemplo de alumna de la primera facultad, o bien las sumamos si se trata de ramas separadas que emergen de un mismo punto, el ejemplo de encontrar un alumno.

Ejemplos

Una universidad está formada por tres facultades:

• La 1ª con el 50% de estudiantes.
• La 2ª con el 25% de estudiantes.
• La 3ª con el 25% de estudiantes.

Las mujeres están repartidas uniformemente, siendo un 60% del total en cada facultad.

¿Probabilidad de encontrar una alumna de la primera facultad?

${\displaystyle P(alumna\ de\ la\ 1^{a}\ facultad)=0,5\cdot 0,6=0,3}$

¿Probabilidad de encontrar un alumno varón?

${\displaystyle P(alumno\ var{\acute {o}}n)=0,5\cdot 0,4+0,25\cdot 0,4+0,25\cdot 0,4=0,4}$ Pero también podría ser lo contrario.

Relación con probabilidad condicionada

Esta herramienta está fundamentada en el cálculo de probabilidades condicionadas.

• Por ejemplo: podemos identificar el 0,6 que encontramos en la rama que va de 1ª facultad a mujer como la siguiente probabilidad condicionada:

${\displaystyle P(mujer\mid 1^{a}\ facultad)=0.6}$

• También esta herramienta se relaciona con algunos teoremas de la probabilidad condicionada

Dado que las tres facultades forman una partición del espacio muestral podemos indicar como:

${\displaystyle \scriptstyle P(alumno\ var{\acute {o}}n)=P(var{\acute {o}}n\mid 1^{a}\ facultad)\cdot P(1^{a}\ facultad)+P(var{\acute {o}}n\mid 2^{a}\ facultad)\cdot P(2^{a}\ facultad)+P(var{\acute {o}}n\mid 3^{a}\ facultad)\cdot P(3^{a}\ facultad)}$

${\displaystyle P(alumno\ var{\acute {o}}n)=0.5\cdot 0.4+0.25\cdot 0.4+0.25\cdot 0.4=0.4}$

Probabilidad de la unión de eventos

Consideremos dos eventos y con probabilidades y , respectivamente. Entonces, tenemos que la probabilidad de su unión, , está dada por

(1)


Esto nos da dos casos importantes a considerar. Cuando y cuando .

Probabilidad de la unión de sucesos compatibles

Decimos que dos eventos y son compatibles cuando contienen al menos un evento elemental en común. En otras palabras, si ambos consideran al menos un mismo resultado.

Cuando dos eventos y son compatibles, su intersección no es vacía (es distinta del conjunto vacío, ). Esto es

.

En este caso, como la intersección no es vacía, y sus elementos (resultado que considera) pertenecen al espacio muestral, se tiene que . Así, consideramos la ecuación (1) para calcular la probabilidad de .


.

Ejemplo

Consideremos el experimento de lanzar un dado y los siguientes eventos:

Que al lanzar el dado el número sea un múltiplo de tres,

Que al lanzar el dado caiga en el número , .

Notemos que , por lo tanto, son conjuntos compatibles. Además, tenemos que y . Aplicando la fórmula de la ecuación (1), tenemos que



Probabilidad de la unión de eventos incompatibles

Decimos que dos eventos y son incompatibles cuando no tienen ningún elemento en común. En otras palabras, si un resultado que es considerado en no está en y viceversa.

Otra forma es que dos eventos y son incompatibles cuando su intersección es vacía (es el conjunto vacío, ). Esto es

Tenemos que la probabilidad del conjunto vacío es ya que este evento no considera ningún resultado. Notemos que, debido a esto, tendríamos que la ecuación (1) se reduce a

(2)