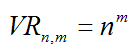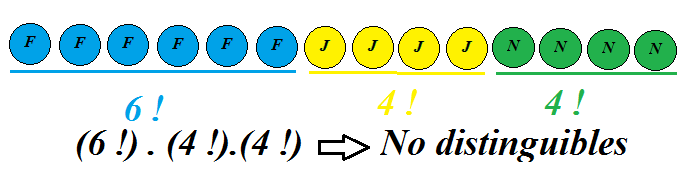Combinatoria

FACTORIAL DE UN NÚMERO (Factorial de un número )

 El factorial de un número entero positivo se define como el producto de todos los números naturales anteriores o iguales a él. 

Se escribe n!, y se lee "n factorial". (Por definición el factorial de 0 es 1: 0!=1) 

Por ejemplo, 5! = 5·4·3·2·1 = 120 Su utilidad estriba en que se utiliza en la mayoría de las fórmulas de la COMBINATORIA

•  2.1. NÚMEROS COMBINATORIOS (Número combinatorio )

 Los números combinatorios se utilizan para establecer agrupaciones en las que no importa el orden y los elementos no se pueden repetir, es decir, para calcular directamente las combinaciones. Se representan así: , y se lee "n sobre p". Por ejemplo, (49 sobre 6) es el número de combinaciones posibles en la “primitiva”. 

• 2.2. CÁLCULO DE NÚMEROS COMBINATORIOS , donde n! es el factorial de n. ¿Qué es la Combinatoria? La Combinatoria es la parte de las Matemáticas que estudia las diversas formas de realizar agrupaciones con los elementos de un conjunto, formándolas y calculando su número. Existen distintas formas de realizar estas agrupaciones, según se repitan los elementos o no, según se puedan tomar todos los elementos de que disponemos o no y si influye o no el orden de colocación de los elementos: 

• Variaciones sin repetición. 

• Variaciones con repetición. 

• Permutaciones sin repetición

. • Permutaciones con repetición.

 • Combinaciones sin repetición. 

• Combinaciones con repetición. 

Variaciones sin repetición Imaginemos una carrera de 100 metros lisos en las olimpiadas. Nos preguntamos por las distintas formas en las que se pueden obtener las medallas de oro, plata y bronce. Este problema sin duda se puede resolver sin necesidad de conocimientos previos sobre combinatoria. Pensemos que disponemos de tres puestos. Para el primero se puede elegir a cualquiera de los ocho participantes. Para el segundo, no puedo elegir al que ya está elegido para el primero, por tanto solamente podremos elegirlo entre los siete restantes. Para el tercero, siguiendo el mismo razonamiento nos quedarán seis participantes. Ahora aplicando el principio general de recuento al conjunto (O x P x B), el total de resultados posibles para el podium sería 8 x 7 x 6 = 336. 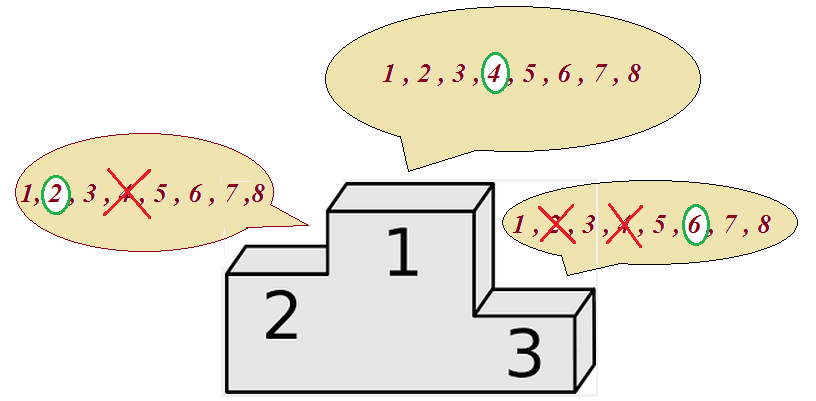En combinatoria, denominamos variaciones ordinarias o sin repetición de n elementos tomados de m en m ( siendo m menor o igual que n) a cada uno de los distintos grupos de m elementos escogidos de entre los n,  de manera que: 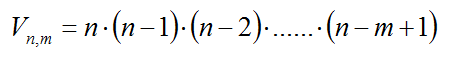En cada grupo, los m elementos sean distintos. Dos grupos son distintos, si difieren en algún elemento o en el orden de colocación. El número de variaciones ordinarias lo representamos Vn,m y se calcula: Variaciones con repetición  Dentro de los juegos de apuestas más populares en España se encuentra sin duda la quiniela de fútbol. ¿Cuántos resultados posibles pueden darse en catorce encuentros entre equipos de primera y segunda división? Este problema puede resolverse también sin conocimientos previos de combinatoria. Imaginamos que cada resultado es un grupo de 14 símbolos y que dichos símbolos solamente pueden ser 1, X o 2. así para el primer signo que pongamos tendremos 3 posibilidades, para el segundo también otras 3 y así sucesivamente hasta llegar al símbolo 14. Ahora no tenemos más que aplicar otra vez el principio general de recuento al conjunto (P1 x P2 x .......xP14). 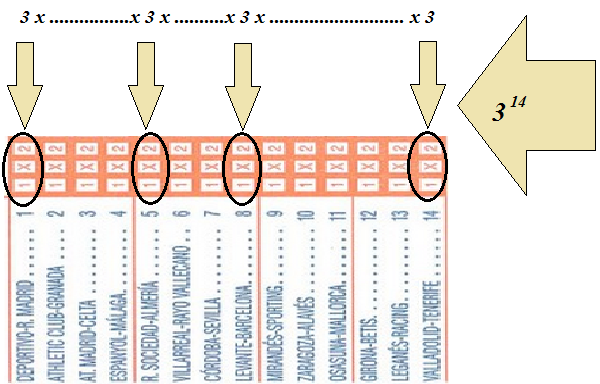Piensa también por ejemplo en: Un entrenador de fútbol dispone  en la plantilla de su equipo de 7 delanteros de la misma calidad y que pueden actuar indistintamente en los tres puestos de ataque del equipo. ¿Cuántas delanteras distintas podría confeccionar? ¿De cuántas maneras diferentes se pueden repartir tres premios distintos entre  Juan, Pedro, María, Alicia y Pilar? En combinatoria denominamos variaciones con repetición de n elementos tomados de m en m, (obsérvese que no hay restricción alguna en cuanto a los valores de n y m), a los distintos grupos de m elementos, repetidos o no, que se pueden formar. Considerando: - En cada grupo hay m elementos repetidos o no. - Dos agrupaciones son diferentes si difieren en algún elemento o en el orden de colocación.    Al número de variaciones con repetición lo notaremos, VRn,m y se calculará: Permutaciones sin repetición Imaginemos cuatro amigos que compran entradas para ver una película. Al sacar estas entradas exigen estar sentados en la misma fila. ¿De cuántas formas diferentes podrán sentarse para ver la película?. Un primer análisis de la situación nos sitúa el problema al mismo nivel del que se resolvió en el epígrafe correspondiente a las variaciones sin repetición. En realidad se trata del mismo razonamiento. La primera butaca la pueden ocupar cualquiera de los cuatro amigos.. La segunda la pueden ocupar cualquiera menos el que ocupó la primera, es decir tres posibilidades , y así seguiremos hasta la cuarta butaca que la podrá ocupar una persona. Aplicando ahora el principio general de recuento al conjunto (B1 x B2 x B3 x B4), el número de posibles agrupaciones sería :  4 x 3 x 2 x 1 = 24 resultados distintos. En la imagen se presentan alguna de las posibilidades. Y mediante un diagrama en árbol podemos representar todas las posibilidades que ocurren en este ejemplo: 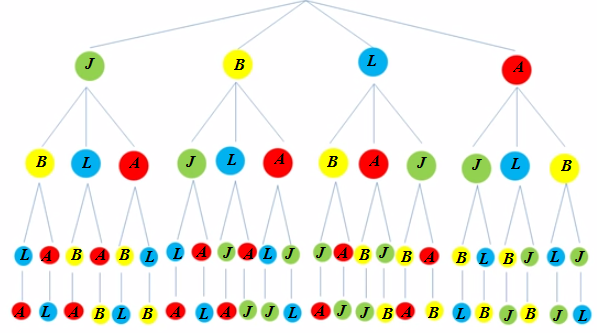Veamos en un vídeo que acontece con seis amigos a la hora de sentarse en una mesa Vídeo enlazado desde YouTube, licencia de YouTube estándar Existen otras muchas situaciones en las que se puede aplicar el mismo razonamiento: ¿ De cuántas formas diferentes se pueden fotografiar 5 amigos frontalmente en línea recta? Un técnico de sonido tiene que unir 6 terminales en 6 conexiones. Si lo hiciera al azar, ¿ de cuántas formas diferentes podría completar las conexiones? De cuántas formas diferentes se pueden introducir cinco cartas diferentes en cinco sobres distintos. Denominamos permutaciones ordinarias o sin repetición de n elementos, a cada uno de los distintos grupos que pueden formarse de manera que: 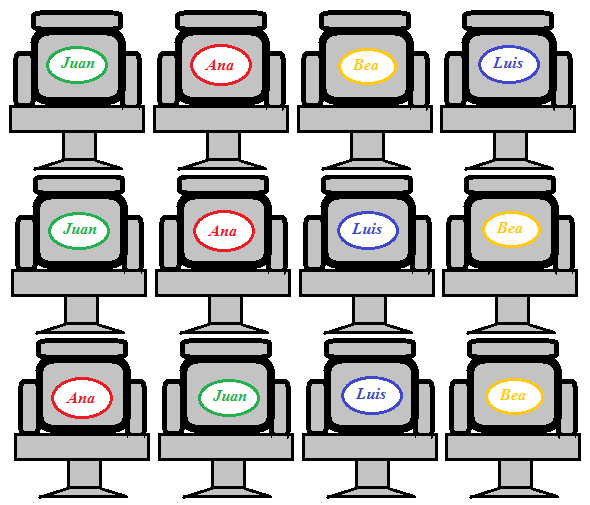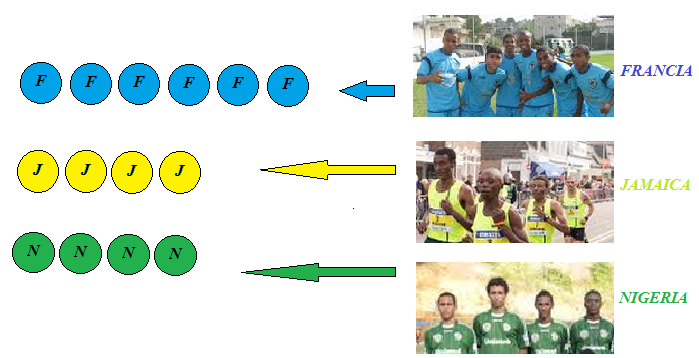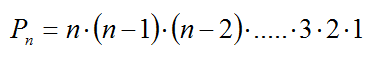En cada grupo entran todos los n elementos. Un grupo se diferencia de otro únicamente en el orden de colocación de los elementos. Al número de permutaciones ordinarias de n elementos lo representaremos por Pn y se calculará: a este  número  lo llamaremos factorial de n y lo representaremos por n! Se utiliza tanto que aparece como tecla directa en todas las calculadoras científicas. 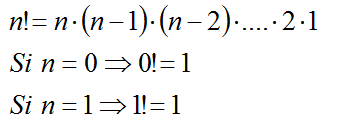Permutaciones con repetición Imaginemos ahora una carrera por equipos. Es decir, una carrera en la que lo importante es el país por el que participas y no el atleta individual. Si en esta carrera intervienen 6 atletas franceses, 4 atletas jamaicanos y 4 atletas nigerianos. ¿De cuántas maneras diferentes puede acabar la carrera atendiendo solamente a los equipos? Este caso lo podemos simplificar la situación  identificando los atletas mediante las iniciales de sus respectivos países. FFFFFF, JJJJ , NNNN. El problema es por tanto buscar todas las formas posibles de ordenar en la misma fila 6 efes, 4 jotas y 4 enes. A continuación puedes observar como se irían confeccionando algunas de las ordenaciones. Piensa por un momento que si cerraras los ojos y te cambiaran de lugar dos letras iguales, si los abres no percibirías ningún tipo de cambio. Por ello necesitamos contar todos los casos en los que no distinguiríamos las ordenaciones si cambiamos de lugar letras iguales Todo ello nos conduce a la definición de Permutaciones con repetición:  Denominamos permutaciones con repetición de n elementos en los que uno de ellos se repite "a" veces, otro "b" veces y así hasta el último que se repite "k" veces (a+b+c+...+k = n) a todas las ordenaciones posibles de estos n elementos. Consideramos dos ordenaciones distintas si difieren en el orden de colocación de algún elemento (distinguible).   Denotaremos a este tipo de permutación como: 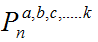       y su cálculo se efectúa como: 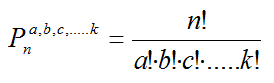Combinaciones sin repetición Y de repente ¡deja de importar el orden! Todas las semanas Loterías y Apuestas del Estado organiza un sorteo consistente en la elección de seis números de un total de 49 posibles. El juego es muy sencillo puesto que se gana premio si la combinación que tú has elegido coincide con la que públicamente y aleatoriamente se realiza ante notario mediante un procedimiento consistente en la extracción sin reemplazamiento de seis bolas de un bombo en el que están las 49. Analizando un poco la situación nos damos cuenta que dos personas que señalen los mismos seis números pero en distinto orden, en realidad tienen la misma apuesta. es decir las 6!=720 formas distintas en las que se pueden seleccionar seis números se tendrán que identificar como una sola. Por tanto para localizar todas las posibles apuestas, dividiremos V49,6 entre las P6 . Existen multitud de situaciones parecidas en las que necesitamos conocer el número de agrupaciones en las que NO IMPORTA EL ORDEN. Por ejemplo: Seleccionar cuatro alumnos de una clase que irán de excursión o repartir cinco entradas entre diez amigos para ir a un concierto. Denominamos combinaciones ordinarias o sin repetición de n elementos tomados de m en m,  (siendo m menor o igual que n) a las distintas agrupaciones de m elementos de manera que: 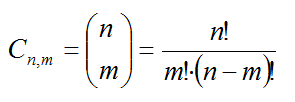En cada grupo entren m elementos distintos. Dos grupos son distintos si difieren en algún elemento. El número de combinaciones ordinarias de m elementos tomados de m en m ,lo denotaremos Cn,m y se calcula: Se puede observar fácilmente que: Las combinaciones sin repetición de n elementos tomados de m en m, podrían formarse a partir de considerar las variaciones sin repetición de n elementos tomados de m en m y posteriormente identificar las posibles reordenaciones de una agrupación, (permutaciones de m elementos), como una única ya que el orden no interviene en la agrupación que estamos considerando; esto es: 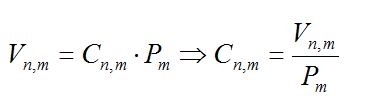Propiedades de los números combinatorios Los números combinatorios aparecen muy frecuentemente en multitud de situaciones en Matemáticas, Física, Biología, etc...Figuran como tecla directa en cualquier calculadora científica. Como propiedades más interesantes merecen destacarse: 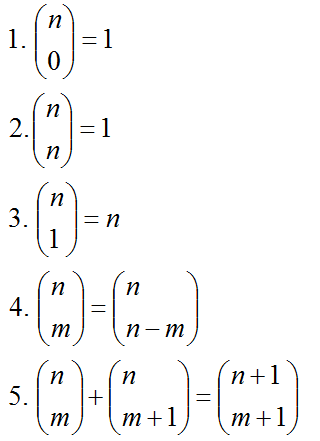Cuando no existían calculadoras científicas, el cálculo de números combinatorios requería de un trabajo complicado. El triángulo de Pascal permitía de una forma recurrente y muy fácil calcular cualquier número combinatorio, aunque es verdad que para cantidades elevadas también era bastante engorroso.