Polinomio

Suma de polinomios

Para realizar la suma de dos o más polinomios, se debe sumar los coeficientes de los términos cuya parte literal sean iguales, es decir, las variables y exponentes (o grados) deben ser los mismos en los términos a sumar.

Método 1 para sumar polinomios

Pasos:

1 Ordenar los polinomios del término de mayor grado al de menor.

2 Agrupar los monomios del mismo grado.

3 Sumar los monomios semejantes.

Ejemplo del primer método para sumar polinomios

Sumar los polinomios P(x) = 2x³ + 5x − 3, Q(x) = 4x − 3x² + 2x³.
Método 2 para sumar polinomios



También podemos sumar polinomios escribiendo uno debajo del otro, de forma que los monomios semejantes queden en columnas y se puedan sumar.

¿Necesitas un profesor de matematicas?

Ejemplo del segundo método para sumar polinomios

Sumar los polinomios P(x) = 7x4 + 4x² + 7x + 2, Q(x) = 6x³ + 8x +3.

Resta de polinomios

La resta de polinomios consiste en sumar al minuendo el opuesto del sustraendo.

Multiplicación de polinomios


1. Multiplicación de un número por un polinomio

La multiplicación de un número por un polinomio es, otro polinomio. El polinomio que se obtiene tiene el mismo grado del polinomio inicial. Los coeficientes del polinomio que resulta, son el producto de los coeficientes del polinomio inicial, por el número y dejando las mismas partes literales.
Ejemplos:

13 · (2x³ − 3x² + 4x − 2) = 6x³ − 9x² + 12x − 6

22(3x³ + 4x² + 2x − 1) = 6x³ + 8x² + 4x − 2

. Multiplicación de un monomio por un polinomio

En la multiplicación de un monomio por un polinomio se multiplica el monomio por todos y cada uno de los monomios que forman el polinomio. Recordar que primero debemos multiplicar signos, posteriormente multiplicar los monomios correspondientes, para lo cual, se debe multiplicar los coeficientes, y luego, realizar la multiplicación de la parte literal, en donde, al multiplicar variables iguales los exponentes se sumarán.

Ejemplo:

3x² · (2x³− 3x²+ 4x − 2) = (3x² · 2x³) - (3x² · 3x²) + (3x² · 4x) - (3x² · 2) = 6x5− 9x4 + 12x³ − 6x²
División de polinomios

Abordaremos la explicación con un ejemplo.

Ejemplo:

Resolver la división de los polinomios P(x) = x5 + 2x3 − x − 8, Q(x) = x2 − 2x + 1.

P(x) : Q(x)

1)A la izquierda situamos el dividendo. Si el polinomio no es completo dejamos huecos en los lugares que correspondan.




2)A la derecha situamos el divisor dentro de una caja.

3)Dividimos el primer monomio del dividendo entre el primer monomio del divisor.

x5 : x2 = x3

4)Multiplicamos cada término del polinomio divisor por el resultado anterior y lo restamos del polinomio dividendo:




5)Volvemos a dividir el primer monomio del dividendo entre el primer monomio del divisor. Y el resultado lo multiplicamos por el divisor y lo restamos al dividendo.

2x4 : x2 = 2 x2





6)Procedemos igual que antes.

5x3 : x2 = 5 x



7)Como en los pasos anteriores, dividimos por , y obtenemos .

Multiplicamos por cada término del divisor y obtenemos:




Procedemos con la resta:





10x − 16 es el resto, porque su grado es menor que el del divisor y por tanto no se puede continuar dividiendo.

x3+2x2 +5x+8 es el cociente.


Factorizacion
Si no hay término independiente


Si no hay término independiente hay que sacar factor común. Sacar factor común de una suma (o resta) consiste en trasformarla en un producto.

Aplicaríamos la propiedad distributiva:





Ejemplo de factorización de polinomio sin termino independente


Descomponer en factores sacando factor común y hallar las raíces.


1


La raíces son: y


2

Sólo tiene una raíz porque que el polinomio, , no tiene ningún valor que lo anule. Como la es al cuadrado, el resultado siempre será un número positivo, entonces es irreducible
Doble extracción de factor común


1

Sacamos factor común de y .

Como es ahora un factor común, sacamos factor común de .



La raíces son y .

Si tenemos un binomio

Cuando tenemos un binomio, puede ocurrir alguno de los siguientes casos:

Diferencia de cuadrados

Una diferencia de cuadrados es igual a suma por diferencia.



Suma de cubos



Ejemplo de ejercicio con suma de cubos:



Diferencia de cubos


Primer ejemplo de la regla de Ruffini


Dividir:

1)Si el polinomio no es completo, lo completamos añadiendo los términos que faltan con ceros.



2)Colocamos los coeficientes del dividendo en una línea.



3)Abajo a la izquierda colocamos el opuesto del término independiente del divisor: .






4)Trazamos una raya y bajamos el primer coeficiente .











5)Multiplicamos ese coeficiente por el divisor y lo colocamos debajo del siguiente término .











6)Sumamos los dos coeficientes .












7)Repetimos el proceso anterior et ).












Volvemos a repetir el proceso et (.










Volvemos a repetir et .










8)El último número obtenido, , es el resto.


9)El cociente es un polinomio de grado inferior en una unidad al dividendo y cuyos coeficientes son los que hemos obtenido.


Cociente:

Resto:


Teorema de Gauss

El teorema de Gauss nos dice que las posibles raíces de un polinomio se obtienen mediante del cociente entre los divisores del término independiente y los divisores del coeficiente principal (coeficiente del término de mayor grado).

Por ejemplo, imaginemos que tenemos un polinomio de grado 4:



Sus posibles raíces serían todos los cocientes de cada divisor de el coeficiente e y cada divisor del coeficiente a:



Tendríamos que ir realizando los cocientes de todas las combinaciones de cada uno de los divisores del término independiente entre cada divisor del coeficiente principal.

Para calcular cuales de estas posibles raíces corresponden a las raíces del polinomio, aplicamos el teorema del resto, es decir, serán raíces aquellas que hagan que el valor del polinomio sea cero.

Una vez obtenidas las raíces, el polinomio lo podemos expresar como:



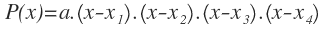
Donde a es el coeficiente principal y los diferentes x1, x2, x3… son las raíces del polinomio. Te recuerdo que el número de raíces de un polinomio coincide con el grado de ese polinomio.