Los fractales son formaciones gráficas que muestran procesos iterativos que tienen una característica en común: repiten procesos infinitos.
Por tanto, podemos concebir una construcción fractal como una figura auto- semejante, es decir, todas sus partes tienen repetición a diferentes escalas.
Los fractales tienen propiedades específicas de alto valor matemático:
Los fractales son construcciones que se generan a través de iteraciones sucesivas, la construcción de un fractal implica la ejecución de un algoritmo que se repite indefinidamente.
Son objetos que se identifican gráficamente y brindan un acercamiento analítico que posibilita explicar sus comportamientos y tienen dimensión fraccionaria.
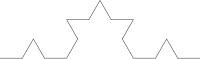
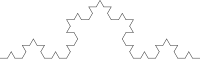
l copo de nieve de Koch, también llamado estrella de Koch o isla de Koch1, es una curva cerrada continua pero no diferenciable en ningún punto descrita por el matemático sueco Helge von Koch en 1904 en un artículo titulado «Acerca de una curva continua que no posee tangentes y obtenida por los métodos de la geometría elemental».23
En lenguaje actual, diríamos que es una curva fractal. Su construcción más simple se realiza mediante un proceso iterativo que se inicia partiendo en tres un segmento de recta e insertando dos más en el tercero medio a manera de un triángulo equilátero, el proceso se repite infinidad de veces. La curva de Koch es un caso particular de curva de De Rham.
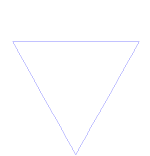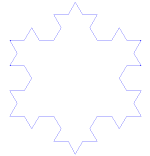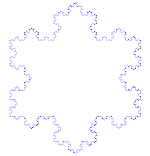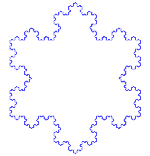
Veamos el proceso que lleva a sustituir cada lado por la llamada curva de Koch: Se toma un segmento, se lo divide en tres partes iguales, se remplaza la parte central por dos partes de igual longitud haciendo un ángulo de 60 grados. Luego, con los cuatro segmentos, se procede de la misma manera, lo que da lugar a 16 segmentos más pequeños en la segunda iteración. Y así sucesivamente. La figura representa las seis primeras etapas de la construcción. La última curva es una buena aproximación de la curva final.
Tres de estas curvas unidas forman el copo de nieve de Koch y el anticopo de nieve de Koch: