El análisis de funciones consiste en el estudio de las características de las mismas a fin de poder describir con precisión los fenómenos que representan. Por ejemplo, si tenemos una función que describe la evolución de la temperatura de un determinado objeto a medida que le suministramos calor, conociendo su máximo y su mínimo podremos saber el rango de temperaturas para el cual estar preparados cuando manipulemos el objeto en cuestión.
El estudio de una función comprende principalmente los siguientes elementos:
Dominio
Recorrido
Ceros
Signo
Monotonía
Crecimiento y decrecimiento
Máximos y mínimos
Curvatura
Concavidad
Convexidad
Puntos de inflexión
Acotación (supremos e ínfimos)
Simetría
Periodicidad
Dominio
Como ya sabes, el dominio de una función es el conjunto de valores para los cuales está definida. Ya hemos visto que se puede restringir el dominio de una función real por distintas razones:
Cuando sea matemáticamente imposible realizar alguna operación con ciertos valores x. Por ejemplo, en la función f(x)=1/x, el valor de x puede ser cualquiera salvo x=0, ya que ningún número se puede dividir entre cero. De ahí que Domf=ℝ-{0}
Cuando el contexto real del que se ha obtenido la función así lo determine. Por ejemplo, en el caso del valor de la fuerza gravitatoria con que se atraen dos partículas, la fuerza puede ser considerada como una función que depende de la distancia entre las mismas, y no tiene sentido que esta sea negativa
Ceros
Los ceros de una función son los puntos de corte con el eje horizontal x. Todos cumplen que f(x)=y=0. Son importantes porque en ellos la función puede cambiar de signo.
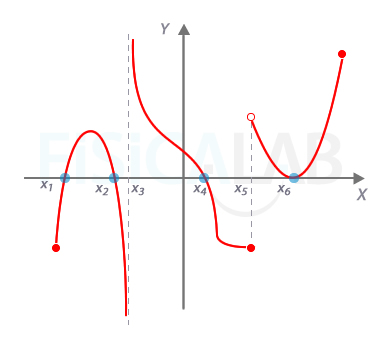
Ceros de la función
La gráfica de la figura representa una función con tres secciones o ramas. En azul se han señalado los ceros de la misma. La rama más a la izquierda cuanta con dos ceros, en x=x1 y x=x2. En la segunda rama, hay un cero, en x=x4. En la tercera rama hay un cero en x=x6.
Observa que en x=x1 la función pasa de ser negativa a ser positiva; en x=x2 y x=x4 pasa de ser positiva a ser negativa; En x=x6 no cambia el signo. Por otro lado, observa que en la asíntota vertical x=x3 y en el cambio de rama x=x5, la función pasa de negativa a positiva sin que haya ningún cero.
Para calcular los ceros:
Si tenemos la expresión analítica de una función (su ecuación), resolvemos f(x)=0
Si lo que tenemos es la gráfica de la función, los ceros son los puntos de corte de la gráfica con el eje x
Signo
Estudiar el signo de una función consiste en determinar el conjunto de valores de x para los cuales f(x)>0, (signo positivo) y el conjunto de valores para los cuales f(x)<0, (signo negativo).
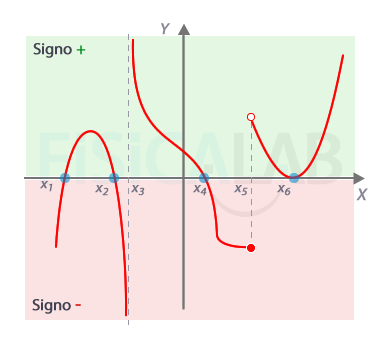
Signo de una función
En la ilustración tenemos, en trazo rojo, la gráfica de una función. Los tramos en los que transcurre por encima del eje x (y>0), son tramos de signo positivo. Estos son: (x1, x2), (x3, x4) y (x6, ∞). Los tramos en los que transcurre por debajo del eje x (y<0) son tramos de signo negativo. Estos son: (-∞, x1), (x2, x3) y (x4, x5).
Para calcular los intervalos de signo constante:
Si tenemos la expresión analítica buscamos los valores de x en los que la función puede cambiar de signo. Estos son:
Los ceros de la función
Las asíntotas verticales (en el caso de las funciones racionales, por ejemplo, los puntos que anulan el denominador)
Los cambios de rama
Éstos valores de x dividen la recta real en varios intervalos. Para averiguar el signo de la función en cada uno de ellos, se elige un valor de x al azar de cada intervalo (xi) y se calcula su imagen (f(xi)). El signo de f(xi) será el signo de la función en ese intervalo.
Si lo que tenemos es la gráfica de la función, los intervalos de signo positivo son aquellos en los que la función queda por encima del eje x, y los de signo negativo, aquellos en los que queda por debajo
Crecimiento y decrecimiento
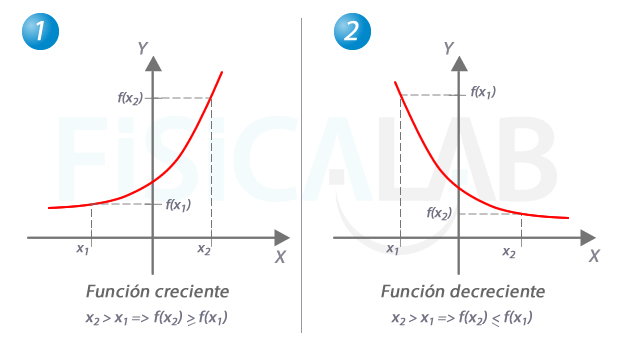
Idea intuitiva de crecimiento
A la izquierda, en 1, un tramo creciente de una función. A medida que aumenta el valor de x aumenta también el valor de y correspondiente. A la derecha, en 2, un tramo decreciente de una función. A medida que aumenta el valor de x, disminuye el valor de y correspondiente.
A la vista de estas ideas intuitivas podemos hacer las siguientes definiciones.
Decimos que una función f(x) es creciente en un intervalo (li, ls) de su dominio si para cualquier par de valores x1, x2 pertenecientes a dicho intervalo y con x2>x1, se cumple que f(x2)≥f(x1). Si además se cumple que f(x2)>f(x1) decimos que la función es estrictamente creciente en ese intervalo.
Decimos que una función es creciente (a secas) cuando lo es en todo su dominio. Igualmente, decimos que una función es estrictamente creciente (a secas) cuando lo es en todo su dominio.
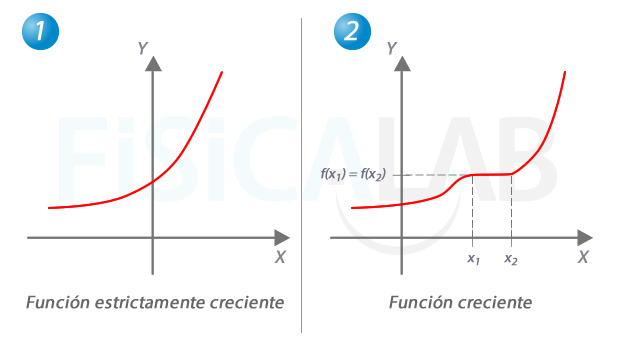
Función estrictamente creciente vs función creciente
A la izquierda, en 1, una función estrictamente creciente. A la derecha, en 2, una función creciente. En esta última puede haber dos valores de x con igual imagen, como es el caso de x1 y x2.
Máximos y mínimos
A los máximos y mínimos se les denomina de manera genérica extremos de la función y pueden ser absolutos o relativos.
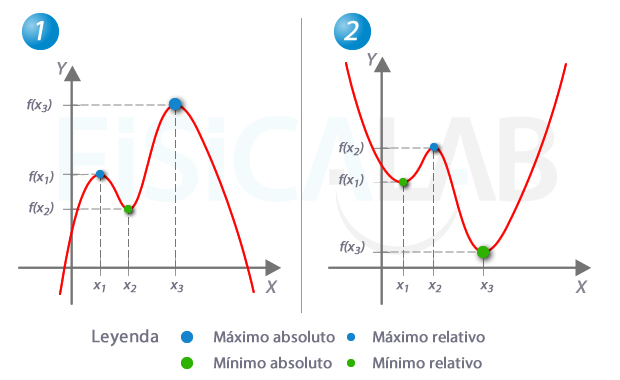
Idea intuitiva de extremos
Observando las dos gráficas de la ilustración resulta inmediato identificar intuitivamente los máximos y los mínimos. Los máximos son los puntos más grandes de la función en su entorno. Los mínimos son los más pequeños. Dado un máximo, cuando el valor de su coordenada y es superior o igual al resto de imágenes de la función, se trata de un máximo absoluto. Si no, es un máximo relativo. Análogamente, dado un mínimo, cuando el valor de su coordenada y es inferior o igual al resto de imágenes de la función, se trata de un mínimo absoluto. Si no, es un mínimo relativo.
Periodicidad
Decimos que una función es periódica cuando su forma se repite cada cierto intervalo llamado periodo. Formalmente:
Una función es periódica de período T si cumple que f(x)=f(x+T) para todo x∈Domf.
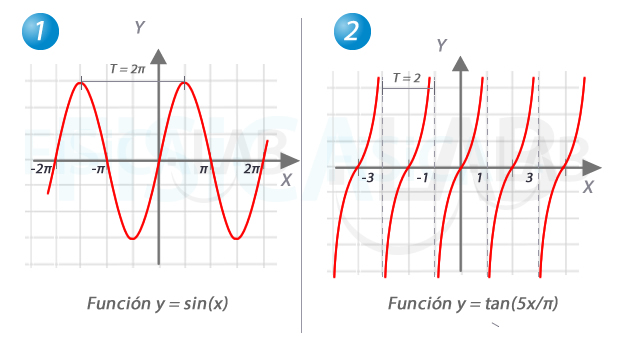
Funciones periódicas
Las funciones trigonométricas son habitualmente periódicas. A la izquierda, en 1, la función seno. Vemos que la forma se repite cada 2π. A la derecha, una variante de la función tangente, cuyo periodo es 2.
Si lo piensas un poco, te darás cuenta que una función que se repite cada T, también se repite cada 2·T, 3·T y así sucesivamente. T sería, por tanto, el período mínimo de repetición, es decir, su período fundamental.
Para calcular si una función es periódica:
Si tenemos la expresión analítica partimos de f(x+T) y estudiamos si existe algún T que haga f(x+T)=f(x). Si existe, la función es periódica
Si lo que tenemos es la gráfica de la función, buscamos si la forma se repite cada cierto intervalo. Si es así, es periódica, y la longitud del intervalo es el período T