Dominio y recorrido de una función
Dada una función real de variable real:
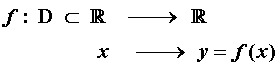
El dominio de la función es el conjunto D ⊂ R de los valores para los que está definida la función. Se representa por Dom f.
![]()
El recorrido o imagen de la función es el conjunto de valores que toma la función. Se representa por Im f.
![]()
Calcular el recorrido de una función
Para hallar el recorrido de una función f(x) hacemos lo siguiente:
1. Igualamos f(x) = y
2. Despejamos la variable x.
3. Estudiamos el dominio de la nueva función.
Funciones periódicas
Una función f es periódica de periodo T > 0 si para cualquier valor de x del dominio de la función se cumple que:
![]()
siendo K un número entero. Simplificando la expresión:
![]()
Es decir, una función es periódica cuando se repite cada cierto intervalo.
Funciones simétricas
Funciones pares
Una función f es simétrica respecto al eje de ordenadas (Y) si verifica que:![]()
Las funciones simétricas respecto al eje de ordenadas se denominan funciones pares.
Puntos de corte con los ejes
Con el eje de abscisas (eje X)
La segunda coordenada debe ser 0, por lo tanto debe ser del tipo (a, 0) . Los valores de a son las raíces de la ecuación f(x) = 0.
Con el eje de ordenadas (eje Y)
La primera coordenada debe ser 0, por lo tanto debe ser del tipo (0, b) . El valor de b se averigua hallando la imagen de 0, es decir, b = f(0).
Solo puede cortar al eje de ordenadas en un único punto.
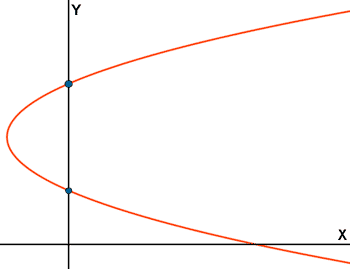
NO es función.
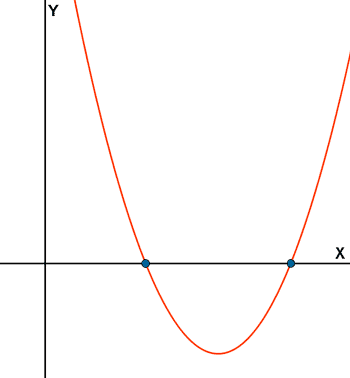
SI es función.
Nos encontramos ante una función cuando la gráfica puede cortar más de una vez al eje X, pero sólo una vez al eje Y. Por tanto, la primera gráfica NO se trata de una función puesto que corta al eje Y dos veces. Mientras que la segunda gráfica SI se trata de una función por cortar al eje Y sólo una vez.
Monotonía de una función
La monotonía consiste en estudiar como aumenta o disminuye la variable dependiente y al aumentar o disminuir la variable independiente x .
Crecimiento de una función
Crecimiento de una función en un intervalo
Una función f(x) es estrictamente creciente en un intervalo (a, b) si para dos valores cualesquiera del intervalo x1 y x2 tales que x1 < x2 , se cumple que f(x1) < f(x2).
Decir que f(x1) < f(x2) es lo mismo que :
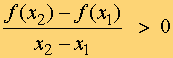
Será creciente si f(x1) ≤ f(x2) , es decir:
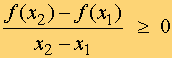
Una función es creciente si al aumentar la 'x' aumenta la 'y' .
Máximos y mínimos de una función
Máximo relativo de una función
Una función f alcanza un máximo relativo en un punto de abscisa x0 si existe un entorno reducido de x0 , es decir E*(x0 , h) = (x0 - h, x0 + h) - { x0 } , tal que f(x) < f(x0) para todos los puntos de dicho entorno reducido.
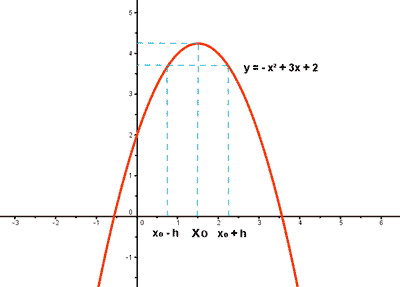
Mínimo relativo de una función
Una función f alcanza un mínimo relativo en un punto de abscisa x0 si existe un entorno reducido de x0 , es decir E*(x0 , h) = (x0 - h, x0 + h) - { x0 } , tal que f(x) > f(x0) para todos los puntos de dicho entorno reducido.
Concavidad y convexidad y puntos de inflexión de una función
Concavidad de una función
Una función f(x) es concava hacia arriba o simplemente concava en un punto, si la recta tangente a la gráfica de f en ese punto está por debajo de la gráfica.
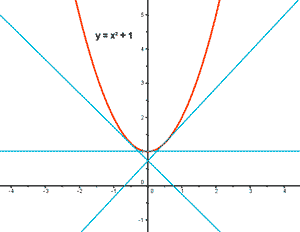
La función f(x) = x2 + 1 es concava puesto que la tangente para cualquier punto queda por debajo de la gráfica de la función.
Convexidad de una función
Una función f(x) es concava hacia abajo o simplemente convexa en un punto, si la recta tangente a la gráfica de f en ese punto está por encima de la gráfica.
Funciones acotadas. Extremos absolutos
Función acotada superiormente. Máximo absoluto
Una función f decimos que está acotada superiormente si existe un número K tal que la imagen de cualquier punto x del dominio de f es siempre menor o igual que ese valor.
![]()
A este número K le llamamos cota superior de la función f .
Una función acotada superiormente tiene infinitas cotas superiores. A la más pequeña de las cotas superiores le llamamos extremo superior o supremo y lo expresamos como sup(f) .
Si la función alcanza al supremo, este se llama máximo absoluto de la función, es decir, que existe x0 ∈ Dom(f) tal que f(x0) = K , siendo K = sup(f) , diremos que f tiene un máximo absoluto y este máximo absoluto es K .
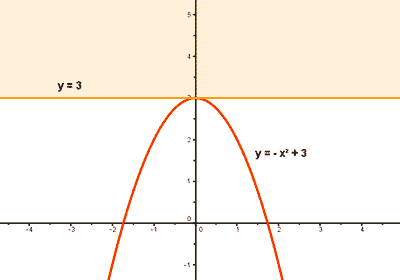
Observando la gráfica, podemos advertir que una cota superior es K= 4 o para toda k>4 es cota superior.
También se puede advertir que la cota superior más pequeña es K= 3 por tanto sup(f) = 3 .
Como K = 3 ∈ Im(f) (K pertenece a la imagen=rango=recorrido de f) tenemos que K = 3 es el máximo absoluto de la función.
Gráficamente, si al trazar la línea horizontal del supremo, esta toca a la gráfica de la función en algún punto, entonces la función tiene un máximo absoluto, y si no toca a la gráfica en ningún punto no tiene máximo absoluto.
Función acotada inferiormente. Mínimo absoluto
Una función f decimos que está acotada inferiormente si existe un número P tal que la imagen de cualquier punto x del dominio de f es siempre mayor o igual que ese valor.
![]()
A este número P le llamamos cota inferior de la función f .
Una función acotada inferiormente tiene infinitas cotas inferiores. A la más grande de las cotas inferiores le llamamos extremo inferior o ínfimo y lo expresamos como inf(f) .
Si la función alcanza al supremo, este se llama mínimo absoluto de la función, es decir, que existe x0 ∈ Dom(f) tal que f(x0) = P , siendo P = inf(f) , diremos que f tiene un mínimo absoluto y este mínimo absoluto es P .
Signo de una función o intervalos de signo constante
Para representar gráficamente una función es útil saber en qué intervalos su gráfica está por encima o por debajo del eje X.
• Si la gráfica va por encima: f(x) > 0
• Si va por debajo: f(x) < 0
Para ello, se deben hallar los puntos de corte de la función con el eje X y los puntos de discontinuidad. Después se estudia el signo de la función en los distintos intervalos en que ha quedado dividido dicho eje.